If you’ve dipped your toes into the world of statistics or machine learning, chances are you’ve heard of Bayesian inference and Maximum Likelihood Estimation (MLE). These two concepts sit at the very heart of how we learn from data. They help us build models, estimate parameters, and ultimately make better decisions under uncertainty.
But what exactly do these methods do? And how do they differ?
Let’s break it down—one concept at a time—without the intimidating math (well, maybe just a little). Whether you’re a student, an analyst, or someone trying to wrap your head around probability, this post is for you.
What Are We Trying to Do Here?
Let’s start with a basic question: What is inference?
In plain terms, inference is the process of learning something about the world based on data. More specifically, we often want to estimate some unknown quantity—like a model parameter—using the data we have.
Here’s the setup:
- You observe some data (say, exam scores or customer purchases).
- You believe the data follows some probability distribution (like a Gaussian, Bernoulli, or Poisson).
- You want to figure out the best estimate of the underlying parameters of that distribution.
That’s where MLE and Bayesian inference come in.
Maximum Likelihood Estimation (MLE)
Imagine you’re a detective. You have a pile of clues (your data), and you’re trying to find the one suspect (parameter value) that most likely produced those clues.
That’s MLE in a nutshell.
The Core Idea:
Choose the parameter that makes the observed data most likely.
Let’s say your data is generated by some process with a parameter θ. MLE asks:

This means: “Find the θ that maximizes the likelihood of the data.”
Why is it called “likelihood”?
Because we’re treating the data as fixed and asking: how likely is it that this data came from different possible values of θ?
It’s important to note: MLE doesn’t care about prior beliefs. It’s purely data-driven. If your data is clean and abundant, MLE often works beautifully.
A Simple Example
Suppose you flip a coin 10 times and get 7 heads. What’s the probability that the coin is fair?
MLE would say:
- Hmm, you got 7 out of 10 heads.
- So the best estimate of the probability of heads (θ) is 7/10 = 0.7.
- That’s the value that makes your observation most likely.
No frills, just logic.
Bayesian Inference: Beliefs + Data
Now enter the Bayesian.
Instead of just asking “What parameter makes the data most likely?”, a Bayesian says:
Let’s combine our prior beliefs with the data to update what we believe about the world.
Here’s the magic formula (Bayes’ Rule):
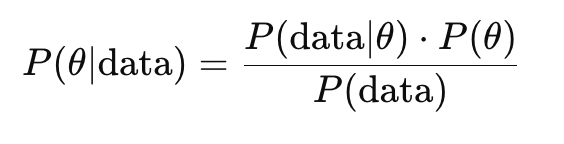
Let’s decode that:
- P(θ∣data) is the posterior: what we believe after seeing the data.
- P(θ) is the prior: what we believed before seeing the data.
- P(data∣θ) is the likelihood: how likely the data is under θ.
- P(data) is the evidence: a normalization constant.
What makes this powerful?
Bayesian inference doesn’t just give a point estimate. It gives you a distribution over possible parameters. That means:
- You can model uncertainty.
- You can include domain knowledge.
- You can update your beliefs over time.
Back to the Coin Flip
Let’s return to our coin.
Say, before flipping, you believe the coin is probably fair. That’s your prior: maybe a Beta distribution centered around 0.5.
After seeing 7 heads in 10 flips, you update your belief using Bayes’ rule.
Instead of just saying “θ = 0.7” like MLE, Bayesian inference gives you a posterior distribution: maybe “θ is likely between 0.6 and 0.8, with some uncertainty.”
That’s richer. It’s more nuanced. And it’s often closer to how we actually reason in the real world.
So Which One Should You Use?
There’s no one-size-fits-all answer, but here’s a cheat sheet:
| Feature | MLE | Bayesian Inference |
|---|---|---|
| Uses prior knowledge | No | Yes |
| Output | Point estimate | Full posterior distribution |
| Computationally efficient | Often | Can be slow or complex |
| Handles uncertainty | Not explicitly | Explicitly models it |
| Works well with big data | Yes | Yes, but slower |
| Works well with small data | Not always reliable | Prior helps stabilize results |
The Philosophical Difference
- MLE is frequentist: It treats parameters as fixed but unknown quantities and relies solely on observed data.
- Bayesian inference treats parameters as random variables with distributions. It’s about belief updating.
Both frameworks are powerful—but they come with different assumptions and philosophies.
When Bayesian Inference Shines
Bayesian methods are incredibly useful when:
- You have strong domain knowledge to encode as a prior.
- You have small or noisy datasets.
- You want uncertainty estimates.
- You’re working in sequential learning or time series, where beliefs evolve.
However, Bayesian inference can be computationally intensive. That’s why modern methods often use sampling techniques (like MCMC) or variational inference to approximate the posterior.
Wrapping Up: Key Takeaways
- MLE finds the most likely parameter value given the data. It’s simple, intuitive, and fast.
- Bayesian inference combines prior beliefs with data to get a full picture of uncertainty.
- MLE gives you a point estimate; Bayesian methods give you a distribution.
- Use MLE when you have lots of clean data and need speed.
- Use Bayesian inference when uncertainty matters or data is scarce.
Final Thought
Bayesian inference and MLE aren’t enemies. They’re just different tools in your statistical toolbox. The more you understand both, the better decisions you’ll make when analyzing data, building models, or solving real-world problems.

